more neurocat Workshops can be found in the official blog
Introduction
I want to show you how to plot graphs with TensorBoard (important for the loss function or basic analysis of your model, e.g. weight distribution). However I don’t want to bore you. So we will also explore TensorFlows ability to create derivatives for a mathematical formula.
Let’s look at the easiest unit possible. A tensor of rank zero. A scalar.
I’m optimistic that you know the derivative of $x ^{2} + 1$. You know the
chain rule and the basic patterns for building a derivative. Python for
example is unaware of these principles unfortunally.
TensorFlow knows the derivative of basic mathematical functions and can
reconstruct the chain rule over the graph structure, similar to you. Therefore
differentiation is an easy task for it.
Why visualization?
You are a human being. You don’t live inside code, but you are a highspeed processor for visual input. When you build a huge computation graph it is often easier to just check if every connection in the graph is established as intended visually, than to search for a mistake in your code. Our visual processing is way faster in that manner. On top of that it’s very cool to have a build in visualization tool without calling e.g. matplotlib. TensorBoard provides visualization of the most important measures in machine learning, e.g. lossfunction, weight density or embeddings from your trainingdata. You get a more efficient understanding of your model reviewing your code from a second visual perspective.
Don’t get me wrong. I also code examples that use matplotlib. Tensorboard is not always the best descision just because it’s build in. Always use the tools that best fit your purpose.
Symbolic Derivatives
Let’s calculate a symbolic derivative together and learn the basics of namescoping and TensorBoard.
We will get warm with importing everything we need and getting to know a TensorFlow placeholder.
import tensorflow as tf
import numpy as np
# initialize a placeholder. It can be feed with values in a session
x = tf.placeholder(dtype=tf.float32, shape=[1], name="x")
A placeholder is also a node in the computation graph. It gives the developer the possibility to feed values into it that propagate over the whole graph.
# create a graph representation of x^2+1
with tf.name_scope("xPow2Plus1"):
We are creating a group of nodes with that command. I want to build a graph representation of $x ^{2} + 1$. As you can imagine that is not just one node in a computation graph. The more nodes the graph has, the more sense it makes to group some of its nodes. It makes sense to group that node and makes the graph easier to read.
The whole group would look like this.
# create a graph representation of x^2+1
with tf.name_scope("xPow2Plus1"):
# square x to get x^2
xPow2 = tf.square(x, name="xPow2")
# create a 1 by initializing a constant feed with a numpy array
npOne = np.array([1], dtype=np.float32)
tfOne = tf.constant(npOne, dtype=tf.float32, name="one")
# add both up to create x^2 + 1
xPow2Plus1 = tf.add(xPow2, tfOne, name="xPow2Plus1")
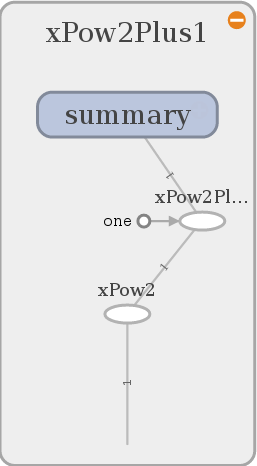
Ignore the summary node for now. This creates a group of nodes looking like that in TensorBoard. The names match the name parameter in each node initialization.
The code has to end with a preparation for later summarizing the value of the resulting node.
# establish the possibility of summarising
with tf.name_scope("summary"):
# reduce to scalar
xPow2Plus1 = tf.reduce_mean(xPow2Plus1)
# summarise scalar
tf.summary.scalar('f', xPow2Plus1)
Nothing special, easy syntax.
We are doing the same with the derivative. Keeping the graph representation hidden for now.
# create a graph representation that is wished to be 2x
with tf.name_scope("2x"):
# compute gradient computation graph
grad = tf.gradients(xPow2Plus1, x, name="2x")
# establish possibility of summarizing
with tf.name_scope("summary"):
# reduce to scalar
grad = tf.reduce_mean(grad[0])
# summarise scalar
tf.summary.scalar('dfdx', grad)
As we see TensorFlow has a build in gradient computation. Taking the node to
be differentiated and the node to be used for differentiation as input it
returns the node for the desired gradient
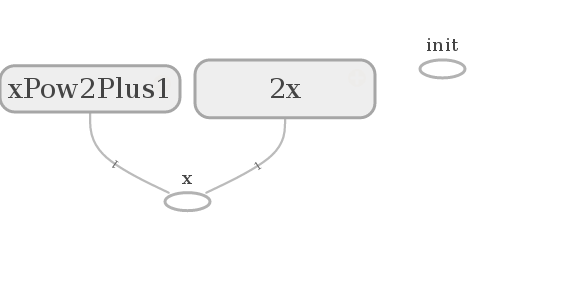
In the end we have to go through our summary routine again. We have now created a
graph that has a feedable node x and two nodes x^2+1 and 2x which we
want to know the resulting outcome of. That’s why we created summary nodes.
In more detail:
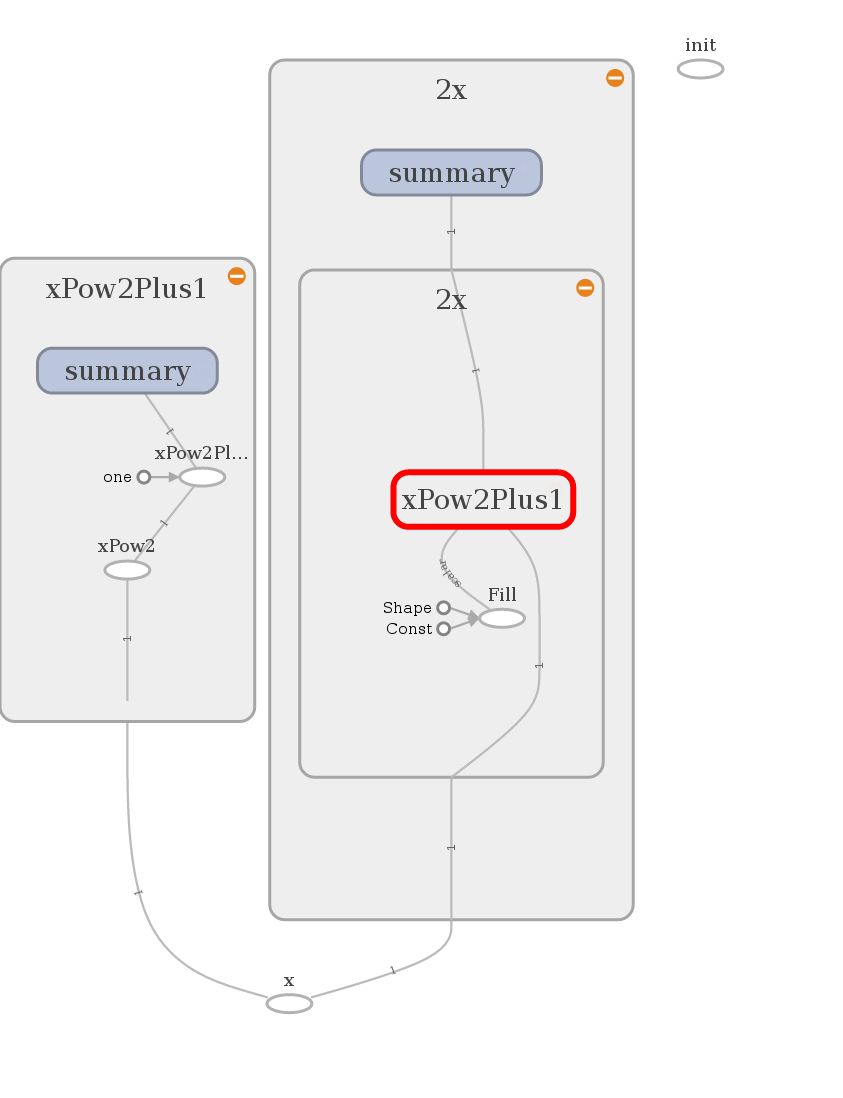
x^2+1 was reviewed above and 2x makes some woodo magic with x^2+1. It
seems to make sense.
The only thing left to do, is to put everything in a TensorFlow session and evaluate the assinged value of the nodes when we feed x with a test set. That’s exactly what we are doing. Because after we formally merged our summary nodes (for usability purpose)…
# for tensorboard usability just merge all summaries into one node
merged = tf.summary.merge_all()
… we have a clear mind to focus on the TensorFlow session:
# create a tensorflow session
with tf.Session() as sess:
# create a writer for tensorboard
writer = tf.summary.FileWriter('./graphs', sess.graph)
You may remember that pattern if you studied my last tutorial. We are
opening a session and a writer for TensorBoard. However, now we get to the tricky
part. I want to loop over a testset (numbers between -7 and 7 with stepsize
0.001) and summarize the node values from x^2+1 and 2x for TensorBoard
visualization. The attentive reader will understand that 2x may not be
$ 2x $, because we just called the TensorFlow gradient computation. We don’t
know the outcome yet. We are just hoping that $ 2x $ will be the outcome.
# create a tensorflow session
with tf.Session() as sess:
# create a writer for tensorboard
writer = tf.summary.FileWriter('./graphs', sess.graph)
# loop through a set of points to draw a graph
for i in np.arange(-7, 7, 0.001).tolist():
# allocate values to the graph nodes
summary, node1, node2 = sess.run(
[merged, xPow2Plus1, grad],
feed_dict={
# feed x with your points from testset
x: np.array([i])
})
# writer takes summary and integer for scalar input
writer.add_summary(summary, i * 1000)
# don't forget to close your poor busy writer
writer.close()
As you can see I feed it with NumPy objects. I looped over the testset that consists of NumPy’s arange, activated the nodes I’m most interested in and added the summary to our TensorBoard writer. Note that I multiplied our second parameter for the summary with 1000. Thats just for convenience because a integer is needed.
Take a look at the graphs. Seems like everything turned out fine: Our nodes seem to represent $x ^{2} + 1$ and $2x$.
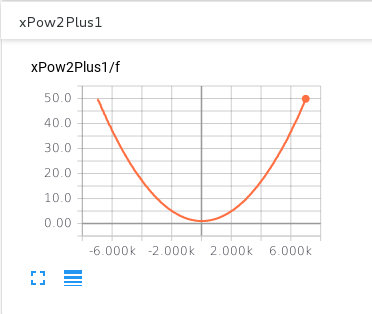
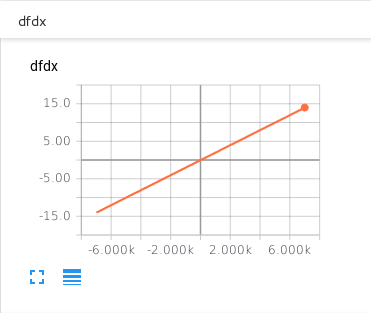
You can also start your TensorBoard deamon with…
florens@neurocat:~/bla/codefolder$ tensorboard --logdir="./graphs"
Starting TensorBoard b'47' at http://0.0.0.0:6006
(Press CTRL+C to quit)
…and navigate with a webbrowse to http://0.0.0.0:6006.
Unfold your scalar plots in the SCALARS section or view the graph by
clicking on GRAPHS.
If you like to know more TensorFlow provides some tutorials itself.
I hope you understood the basic concept of namescoping and got to know a little more about the power of TensorFlow and the advantages of the graph representation. I hope you like the design of TensorBoard and understood the basic usage and are able to find opportunities to use it.
In the next tutorial we will create a MLP. You will learn a playful handeling of namescopes and another example of the use of summaries. On top of that we will, lazy as we are, skip to think about backpropagation or gradient descent, because TensorFlow is smart enough to do that for us.
Have a great code. See you in the next tutorial.
 Music
Music